

In the year 2002 a new theory about the theorem of Pythagoras in Giza was published. Again an author promises to have solvet the “mystery of the Giza-Pyramids”. The author Klaus Schröer was very sure on his – now deleted – website. Rightfully?
The author and his idea are long forgotten since, but because his argumentation and later his excuses are so typical for the whole genre, it is worth to show it.
On a map of the Giza plateau made by the survey expedition of Napoleons between 1798 and 1801, he discovered this relations:
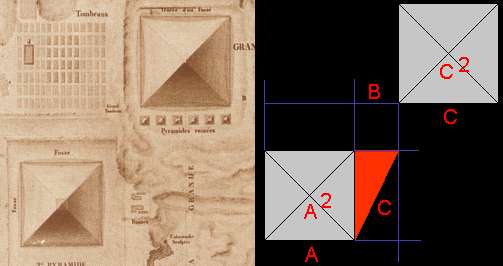
The distance between the eastern side of Kafre's pyramid and the western side of Khufu's pyramid Is exactly as big, that the hypotenuse of the red right angled triangle is as large as the base length of Khufu's pyramid. What does that mean?
|
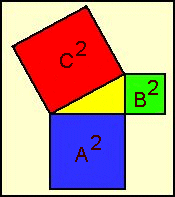
| Fig. 2 – Theorem of Pythagoras |
In a right angled triangle the area of a square constructed with the length of the longest side as large as the areas of the two squares constructed with the two other sides together. In the arrangement Schroer thinks to have found the difference in east/west direction between the two largest pyramids in Giza is exactly as large to construct a right angled triangle were the largest side is as large as the base length of Khufu's pyramid, the second largest side as long as Kafre's, and the smallest side as long as Menkaure's pyramid base length.
To demonstrate this, Schroer makes a geometrical construction with many lines, assisting triangles and circles. Why so complicated? Obviously to obfuscate the reader.
The check is much more simple and faster. If Schroer is right, the necessary distance B of the pyramids can be obtained by a simple calculation If A2 + B2 = C2, B is the square root of (C2 - A2). A2 iis nothing more as the base area of Kafre's pyramid, C2 is the base area of Menkaure's pyramid. If we subtract this from Kafre's base we get the area of a square constructed with the length of B. The square root of this gives the necessary length to fulfil the theorem. The result can be checked against reality.
The baselength of Khufu's pyramid is 230 m (centimetres are irrelevant in this case), Kafre's has a width of 215 m. Dhe difference of the areas is 6675 square meters, the square root gives a necessary distance B of 81,7 meters.
To verify this I took a 1:2000 plan of the Giza plateau[1 ]. With a scale ruler distances can be measured with a precision of about one meter. The distance B between the pyramids is about 110 meters!!!. Over and out, finished. An error of about 30 meters cannot be explained with building mistakes or rounding errors. This bird is dead.
This quick chech showed, that the idea CAN NOT be true. Why didn't the author check this? Well, because, as we could read on his home page, he was interested in toppling over “dogmatic theories of Egyptologists”, but not interested in wasting time with research. The only evidence he consulted was the old map from Napoleon, and a satellite picture on the internet. And with those two pictures it works, so he claims.
|
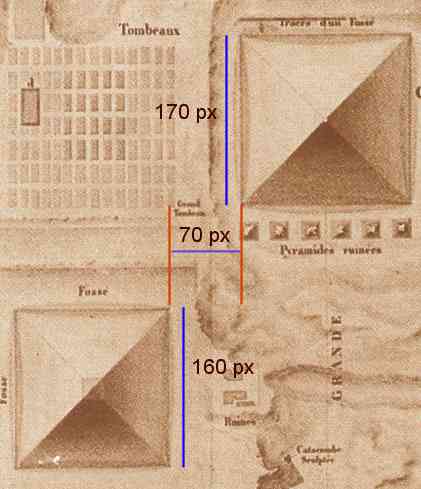
| Fig. 3 – Distances on Napoleon's map |
Really? Well, even without a scale on the map we can check the relations. I simply measured on the map Schroer had linked in his article the base lengths and distances in pixels (px). I got 170 px for the pyramid of Khufu, 160 px for that of Kafre, and a distance of 70 px. Distance2 = 4900, (Khufu2 - Kafre2) gives 3300, the square root is 57.4, about 13 Pixel or 20% to short! Even on the map the author himself used the idea can be disproved in a few seconds.
The same goes for the satellite picture from Spaceimaging. I downloaded the full resolution picture (careful! 3 MB large.) and measured the distance like with the map of Napoleon. The results: pyramid of Khufu 277 -283 px (it is a bit distorted on that picture), p. of Kafre 265 px, distance 150 px. If I use these values in the equation above, I get a necessary distance of 80-99 px. On tis map, too, the formula doesn't work.
Now the author could have spared himself some embarrassment by saying “OK, I made some mistakes and retract my idea” - but that's not the way fringe science works. The genius is never wrong, and when he IS wrong, “the science” is behind it, by hiding the truth or manipulating data. So he produced a bunch of “explanations”, some of them I will show now.
|
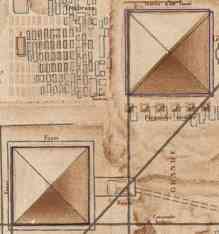
| Fig. 4 - Lehner and Napoleon |
The author first argued, that the measurements in modern works are completely wrong. Only the original map of Napoleon is correct, because the scientists then had no agenda. Later geometers had ideological reasons to fake the correct values because they didn't want to show the superior knowledge of the ancient Egyptians. With the pyramids only a few meters larger, like on Napoleon's map, everything would be all right.
Well, the picture on the left is a combination of a modern map (Lehner, The Complete Pyramids) with the map from Napoleon. Strange: the dimensions of the pyramid are almost the same (dhe modern measurements are 2.5 m smaller than Napoleons measurements, this is smaller than the width of the line), only the positions are a bit different (the modern map places the pyramid 12 meters to the east and 8 m to the south).
The differences are too small for Schroer to draw any advantage from.
After Schroer realised that this discussion lead to nothing, he surprised us with a new original excuse. We just don't know how large the pyramids have been, because stone robbers changed the dimensions. If Khufu's pyramid had only been 11 m wider, everything would be perfect. Even better: if the stone robbers took the stones preferably from the cooler north- and west-side, only 8 m would be necessary to prove his idea. Today Egyptologists believe, that almost 6 m are missing (the average width of the Great Pyramid today is 224 m) , why not 14 m?
Well, when we start an argumentation based completely on “if”s and “maybe”s, we could “explain” everything wished for. In science, such an argumentation is completely worthless.
There are reasons why archaeologists publish the values of the pyramids sizes. For one, there are many of the original casing blocks still in place around the pyramids. When the great destruction began in early Arab times, the pyramid bases were covered in meter high sand dunes. They didn't care about digging them out and removed only the blocks above the dirt level. Here some pictures.


On the left a view along the western side of Khufu's pyramid, on the right some casing blocks stil in their orifinal position on that side. Together with those blocks there are chiselled measurement lines on the foundation which are still visible for long stretches:



On the left you see a casing block and a measuring line on Khufu's west side. The picture in the middle shows the largest casinng block of this pyramid still in place, on the northern side and over 15 tons heavy. The picture on the right show granite casing blocks at Kafre's pyramid. The Arabs tried to split these bocks, not very successful as the remnants around the pyramid show.
To finish this side trip with the best preserved row of casing blocks at Khufu's pyramid, in its north side:

During the excavation of Borchardt in 1925 all four sides of the Great Pyramid were ceared for the first time, so that British egineer J.H. Cole could measure the whole pyramid. He noticed::[2 ]
Dorner made new measurements in 1980, especially on the western side incompletely cleared at Borchardt's time. Dorner notes:
"On the western side are pavement remnants near the northern and southern side … around the middle of this side chiselled lines are visible over a distance of about 60 m, there are also several casing blocks in their original position. ..."[3 ]
Dorner was able to correct Cole's the azimuth angles of the sides for about 20", but confirmed the length measurements with a reduced error interval. We are now sure that the maximum error on all sides is below one centimetre.
There is no doubt, that the Great Pyramid never was wider on any side
The last excuse is one of the best ones I have ever heard in fringe science. The author claimed, that I did not take tectonic activities in account. Due to plate tectonics the pyramids could have drifted apart those 30 meters, and 4500 years ago all would have been perfect.
Obviously he has no idea how plate tectonics works, and that something like the middle oceanic ridge or the rift valley should be visible at Giza. Such features could not be overlooked.
No, this also doesn't work...
Again someone was sure to have solved “the” mystery of the pyramids – and again it was nothing more than a daydream. The examination of the author's excuses took more time than the destruction of his initial idea. The mistakes are clearly visible, can be found within a few seconds with a pocket calculator and a map, and his excuses like the wandering pyramids can be discarded wit some common sense.
The author did not like my review – again a thick headed critic not able to grasp the large picture and the spiritual insight and the connection to the universal wisdom.
Exactly, 42.
| Remarks: | ||
| [1 ] | Maragioglio & RinaldiL'Architettura..., Vol. VI Tavola 1 | |
| [2 ] | Dorner, Josef; Die Absteckung und astronomische Orientierung ägyptischer Pyramiden, p. 70f | |
| [3 ] | ibd. p. 75 | |