

Most secret messages of the great pyramids of Egypt are found in the dimensions of the buildings, but also their positioning on the surface of the Earth should be a sign of higher knowledge of their planners. These mysteries are also often older than 100 years, but as we saw on the previous pages: older is not in every case better. Let's have a look at von Dänikens location mysteries.
|
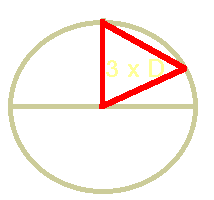
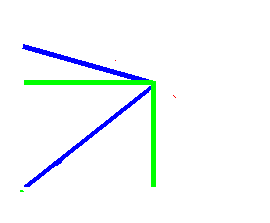
| Fig. 1 – Triangle |
Riddle (11) is: "The distance of the Great Pyramid to the centre of the earth is the same as the distance to the North Pole and is therefore the same as the distance from the North Pole to the Earth's centre"
This is by far the most common „mystery“ of the Great Pyramid and is used in almost any book mentioning pyramid mysteries. It is also one of the most flawed, and that in several aspects.
It begins with the fact that the formulation is simply wrong. What is meant is that the three red lines in the picture alongside have all the same length. The route through the earth from its centre to the pyramids, from the pyramids through the Earth to the North Pole, and inevitably the distance from the pole back to the Earth's centre. But the distance to the pole for us puny men would be the one measured on the surface of the Earth.
It was argued, that this was nitpicking and that it was obvious, that the author meant the triangle. And with this the mystery works.
Unfortunately not, and that because of two reasons. To fulfil the premise the pyramid must stand exactly on 30° North on an ideal spherical Earth. It is, however, about 2.5 kilometres to the south. That is not much, but let us remember that the pyramid is supposed to be a sign of ancient astronauts. We with our technology far inferior to that needed for interstellar travel can already detect incorrect positioning in the centimetre range. Even better, even at the time of Napoleon, already over 200 years ago, the technology was so far developed to detect deviations of less than 100 meters.
As a sign of an ancient alien planning this looks very unsuitable.
Well, told me an English pyramid book author, I was doing quite a large mistake by not taking the elliptical shape of the Earth into account. If I did, everything would be A-OK. Really?
It's true that the triangle equation applies only to perfect circles, which are cross sections of perfect spheres. The Earth is not a perfect sphere, but a spheroid. The cross section is an ellipse, not a sphere. The polar diameter is smaller by several dozen kilometers than the equatorial diameter.

|
| Fig. 2 - Ellipsoid |
A circle has a constant radius. An Ellipse has two extreme values: the “semi major axis” which describes the maximum radius (horizontal line in the picture), and the "minor axis" with which shows the smallest radius (vertical line). An ellipse with the semi major axis of “a” and a semi minor axis of “b” < “a” always fits into a circle wit the radius “a”, as shown in the picture.
So far it is simple to understand. But what about the distances we need? On a circle, 30° North is always at the equidistant point for pole and centre, but never on an ellipse. To calculate the point on an ellipse we need the ellipse equations of mathematics with which the problem can be solved formally.
For the following calculations I use graphs and formulas of this site (Longitude and Latitude Conversions), which explains the derivations pretty well. Let us first look at this chart:
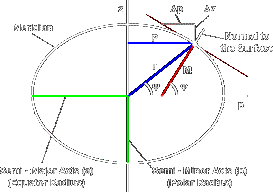
It reveals that the latitude Φ is not identical with the position angle Ψ, because the latitude is defined by the height of the celestial pole above the horizon of a place. This horizon is on an ellipse not perpendicular to the line connecting to the ellipse center, as you can see on the graph. To calculate with the ellipse equations we first have to transform the coordinates.
What we need to determine is the real radius of the latitude circle, P in the picture, and the vertical distance to the equator. With these two values we can , together witn the polar and equatorial radius of the Earth, determine the desired distances r (distance of Giza to the centre of the Earth) and rp, the distance to the north pole.
P is obtqined from the following simple formula (resolved formula (10) an the linked page)
with a as the equator radius (semi major axis) of 6378140 meter, and b as the polar radius of 6356775 meters.
The height of Giza above the equator can be obtained by resolving the ellipse equation
|
| Fig. 4 - Distances |
to z. The distance to the centre of the Earth and the North Pole can each be calculated with the theorem of Pythagoras. The distance to the centre is the square root of (P2+z2), the distance rp to the pole is the square root of ((Polar radius-z)2+P2), because distances are he hypotenuses of a right angle triangle.
For 30° northern latitude (the distance to the real location of the Great Pyramid 2.5 km to the south makes no difference) we get the following values:
| P | Z | r | rp | Difference |
|---|---|---|---|---|
| 5528254 m | 3170392 m | 6372832 m | 6380802 m | 7969 m |
The distance between 30° North and the pole is about 7.969 km longer than the distance to Earth's centre. This is NOT the distance to the equal-distance point, only the difference of the distances!
The real equal-distance point lies several kilometres north of 30° North, whereas the location of the Great Pyramid is 2.5 kilometers south of it!
To find the point where both distances are equal we “only” have to find a P where the hypotenuses of both triangles are equal. I will not resolve these equations here (it is, after all, not a math site), but the necessary latitude, however, is 30,0833° North. The distance on the surface can now be calculated based on the length of a degree of latitude at the latitude 30° North. The web site Length of 1 of Lat and Lon provides the necessary information: 0.0833° are 9234 meters, the looked-for point of equal distance lies about 12 km north of Giza, near the village Embaba at the southern end of the delta of the Nile.
Again, no deal. The score is now 8:11 against the pyramid mysteries.
No problem for the above mentioned author. He had another hypothesis about a “pyramid belt”, and while my results battered one hypothesis, it supported his other one, where he elaborates that the real PLANNED pyramid location was some kilometres north of Giza (and that the super-intelligent pre-Egypt-Egyptians were obviously only to stupid to build there). Another author was really enthusiastic because he had “found out” that the planned pyramid location must have been 30.06° North (and the architect got the plans wrong), and since 30°083°N is not too far away he saw this as a manifest of the knowledge of the ancient Egyptians.. And since the delta of the Nile was an artificial construction for him, the position of the equal-distance point at its apex was again the celebration of this antique wisdom.
Her we se again the flexibility of alternative science: one theory falls flat on the stomach – but don't worry, they have many more in the sleeve...
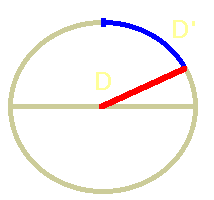
|
| Fig. 5 - Arc |
Before anyone argues that the claim works with the distance on the surface, here a small calculation on a perfect sphere.
The real distance we had to travel on the surface is the arc D', which is, as we can see in the sketch, much longer as the mathematical tendon between the two points. About 400 km to be exact, and also 400 km longer than the distance to Earth's centre. To stand on the equal-distance-point the pyramid must be standing where the arc has the same length as that distance to the center. That would be near the coast of Turkey in the Mediterranean.
With an error that large we don't need to solve any ellipse equations for the real form of the Earth, that would make only a difference of a few kilometres.
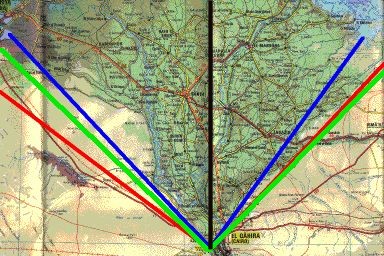
Riddle (4) says: "The pyramid angles divide the delta region of the Nile in two equal halves"
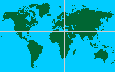
The delta is the mouth of the Nile, a fertile, fan-shaped region where the Nile splits into dozens of branches. But which delta is meant? The delta today? Or 150 years ago? Or the delta 4500 years ago? That the allegation is not true with today's Delta shows the map on the left: The western side everything left of the vertical black line) has undoubtedly far more area than the eastern side! (The pyramid stands at the intersection of the lines).
It is impossible to determine today how the delta region looked like 5000 years ago. So this statement is nothing more but utterly pointless – except the Theosophists of the 19th century had a time machine to travel back to the time of Khufu.
Another related claim is that the diagonals of “the” pyramid encloses the whole delta of the Nile. But what does “enclosing of the delta” mean? It can be the maximal angle which encloses all the irrigated land and all side channels (red lines) or the eastern- and westernmost mouths of the river's branches (blue lines).
On the first glance you can see that the pyramid (at the intersection of the lines) stands asymmetrical to the Nile Delta. You had to place it about 20 kilometres to the east in the Mokkatam mountains to be at the apex. Also, the wider opening that encloses all branches of the delta, has an angle of much more than 90°, whereas the second definition requires an angle less than 90°. Neither “enclosin” definition meets the necessary 90° - the angle the diagonals of the pyramid form.
The angles they form are the green lines – they are wider than the delta in the east, and do not enclose the whole western delta. They are somewhere in between – and definitively no sign for any supernatural mystery.
BTW: There are other pyramids that fit the requirements much better than the “Great One” in Giza. South of Giza the Nile turns east, so the pyramids of el-Aryan and Abusir enclose the delta much better.
Funny: The riddle even doesn't work with the original picture of the inventor, Piazzy Smyth. You can see river branches runnimg out of the marked section to the east and to the west, and the marked fruit land borders are almost completely out of the marked sector.
New score: 7:12 for pyramid mysteries.
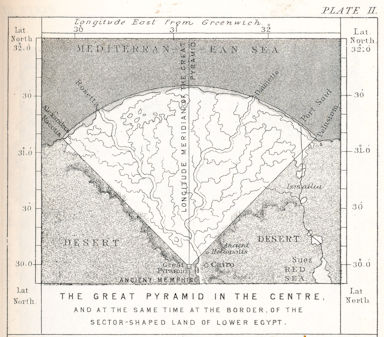
Riddle (2) says: The Pyramid lies in the centre of the land masses of the Earth. The statement is very unclear since no explanation is given what it really means.
The original source, Piazzi Smyth, writes, that the meridian going though the Great Pyramid is the longest one going over land, and that the circle of latitude is also the longest possible going over land. The pyramid therefore lies on the crossing of both longest possible lines and is therefore at the mass centre of all continents of the earth.
This shows that this riddle is an equivalent to riddle (3b):
This meridian is also the longest North-South-meridian going over land and forms a natural zero point for measuring the longitude of the entire globe.
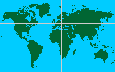
The picture above shows it. The vertical and horizontal lines show, according to Smyth and Däniken, the longest possible parallel and meridian across land. But that is not true, and everyone can check that with a modern globe.
The longest meridian (the semi-circle from pole to pole) lies about 250 km west from Giza and runs about 2000 km longer over land than the one at Giza. What is the reason for that mistake? Well, there aree different reasons, but the main reason is: Smyth, the originator of that riddle, ignored Antarctica. To be more precise: at his time the existence and the dimensions of Antarctica were completely unknown. The riddle dates to the mid-19th century, the first land belonging to Antarctica was discovered in 1821. During the next decades more and more parts were discovered by whale hunters and discoverers, but if all those parts belonged to one continent or if they were individual islands was not known then.
Today we know the dimensions, and if we put them into measurement, the riddle falls apart.
|
| Fig. 8 - Reality |
The parallel going through Giza is also running shorter over land than the parallels to the north going over the whole of Asia. According to my measurements, 50° North would be the best candidate, running more than 2000 km over land than the one trough Giza. The “real” center of the landmasses would then be some kilometers west of Kiev at the Black Sea. In the Ukraine. You can check this with a little patience and a globe. Where did Smyth makes his mistake here? Easy, he didn't took the distortion of a flat map into account.

|
| Fig. 9 - Projection |
To the dismay of cartographers, Earth is not flat. Yes, it nearly a sphere, and that is known for more than 2000 years now. And it is impossible to flatten a sphere without distortions an tears. The only way is to make a projection, all our maps are therefore projections of the globe. You can visualize this process by imagining a point light source in the center of a wire-frame globe. Put a cylinder of paper around it and retrace the shadows cast by the wire-continents- So you get a typical projection on the paper.
If you make a cylindrical projection like the common Mercartor-projection, the horizontal distances are stretched on the map to larger and larger lengths north and south of the equator, whereas the vertical distances stay constant. To get the horizontal distances right you have to multiply the length measured on the map with the sine of the latitude. A length o the map that represents one kilometer on the equator is 1.3 kilometers long at 50° latitude. Without correcting the distances one cannot use the centimeters on a map to measure a correct distance.
Even on a globe itself there are problems. Because of the form of the earth, a degee on the equator is longer than north or south of It, so one cannot only measure the degrees a parallel is running over ground. One has to correct it- a fact Smyth simply ignored, as all the other writers copying his claim for the last 140 years.
After I published the refutation of this riddle, some riddle-supporters protested and tried to re-interpret Smyth's original formulation to still make it true. They argued, that he meant in reality the gravity center of the flattened land-masses, the center of an integration over the whole area.
I made some rough calculations many years ago and found out, that the real gravity center is at least 100 km to the east. Fortunately, someone else did the real work then, with a computer simulation. On Holger Isenberg's Mars Conspiracy Pages we find the result of his calculations[1]: The real center of gravity is on the meridian 35° East, about 450 km east of the pyramids.
Since he wanted to believe in this riddle he argued, the water level must have been different. And yes, he found out that the pyramids are really the center if the water table was about 150 m higher than today. So the lower 50 meters of the pyramids must have been built by using scuba-gear. Whatever...
Since we are already here, we can resolve another “riddles” en passan: the land divider. In riddle (3a) Däniken writes: The meridian running through Giza divides the oceans and the land masses in two equally large parts.
This can only be true, if the gravity center of the land masses is on this meridian. As we saw, it doesn't, so this riddle is also disproved.
It looks bad for Däniken's riddles, only four are left open, 15 have been solved so far. In plain numbers: 4:15 against pyramid riddles.
This riddle is not listed above, but I have to inlude it because it is so funny. On page 156 in his Die Augen der Sphinx (The Eyes of the Sphinx) he writes:
"I placed a large world map on the floor, took a large ruler and knelt down. [...] My grotesque play brought strange results [well, at least he sees it, note FD :-)] on the living room floor when I drew a diagonal. The line running through the pyramid from south-west to north-east ist the longest possible line across land on the whole globe."
As already explained above, you can not get correct distances from a map without transformations. With angles that is even more problematic, because you get additional angular distortions depending on the sort of projection used for the map. What Däniken measured as “diagonal” on the map, is on the globe a sine-curve. A correct distance measurement can only been done on a globe measuring a “great circle” running through Giza with an azimuth of 45°. Such a circle runs about 12000 km across land – and is, as we have seen above, not the longest possible line across land, since the parallel at 50° North runs 4000 km more across land.
This is not a location mystery, but it relates to the Great Pyramid and its surroundings, therefore I put it here.
Again, this mystery is old, for the first time published in 1902 by the English mystics John Cotsworth in his book The rational Almanac. And, again, modern authors discussing this riddle in their books do not know the original definition of it. Why research the background, if it already sounds mysteriously enough?
Däniken writes about riddle (9):
"(a) The pyramid is a giant sundial. The shadow cast by it between mid-October and early March shows the length of the seasons and of the year.
(b) The length of the stone slabs that surround the pyramid corresponds to the length of the shadow of one day.
(c) observation of this shadow on the flagstones, the length of a year was specified to the 0.2419. part of a day."
This passage troubled me a bit: "The shadow cast by it between mid-October and early March". So this fantastic sundial can only be used for about four and a half months of the year, or how should I understand it? If so, is it not a huge waste of resources, to build such a gigantic building for such a limited use?
But more on that later. Let's look first at the period in which the pyramid can be undoubtedly used as a sundial.
|
| Fig. 10 - Sundial |
The most primitive form of a sundial is a shadow stick or gnomon. This is a stick vertically put in the ground. It casts a shadow wandering synchronous to the movement of the sun in the sky, and by preparing markings on the ground we can use it to read the time of the day.
.
Since the sun is at 12:00 hours (noon local time) exactly in the south and highest in the sky, you can use this as a central point of the dial. Sounds really all quite simple
.
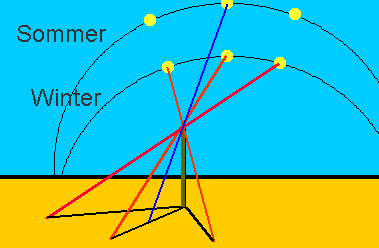
But as so often, the devil is in the details. During the day, the sun describes an arc in the sky and changes its height permanently. But this arc ist not constant, it changes every day due to the tilt of our Earth's axis. In the summer the sun is higher and shinses longer than in the winter. The difference of the noon position changes for about 47° each year! This is an important point for our subsequent considerations.
The effects are far reaching. Due to the changed course of the sun, the direction of the shadow cast by the stick cast at a specific time changes every day. Only the south position at 12:00 hours remains constant.
.
To use sundials with a vertical pointer,we cannot use the direction of the shadow, but only the shadow of the tip, in combination with complicated "corrected" dials with contour lines for each season.
The Egyptians used sundials. These were simple ones with no complicated dials, the so-called horizontal sundials. These were simple bars, oriented east/west, with a T shaped pointer in the middle. With 12 lines across the bar the day between sunrise and sunset is divided in 12 periods. These “hours” changed their length during the seasons, but the Egyptians didn't care.
A solution would be an equatorial sun dial, where the dial is oriented parallel to the Equator. With such a construction the direction of the shadow would be the same for each hour throughout the year. Or one uses a triangular pointer, which does look similar to a pyramid, but needs in Giza an inclination of 30°, and not the 52° of the pyramids. The only way to use pyramids as sun dials is using the shadow of the tip, like with a primitive stick in the ground. A stupid design for hyper-intelligent space aliens, as we shall see shortly.

|
| Fig. 11 – Shadow of the Great Pyramid |
In 1997, I traveled to Egypt in late November, and took some time on the last day of November to watch the shadow of the tip of the Great Pyramid.
.
One could see how the shadow got shorter and shorter when the sun rose, and long before 12 o'clock it was so short that one couldn't see a tip at all. The shadow was just a small dark stripe across the northern base of the pyramid.
One hour later the situation was not much better. The picture above was taken five minutes before one o'clock. The shadow of the tip of the pyramid is smeared up across an area approximately 5 m wide, and the shadow itself is extremely smudged. The photo enhances the contrast, the naked eye was unable to define the center of the shadow. This is not because of the now missing top of the pyramid, its size would have no influence on the result.
I took some stones as alternative dial and tried to determine, when one was definitively was in the shadow, and got a time span of about 10 minutes when I could be really sure. For such a huge sundial whih was built during 20 years rather disappointing.

|
| Fig. 12 – Shadow again |
After one o'clock the situation even gets worse. The picture on the left shows the shadow at the end of November at about 13:05 hours – the shadow of the tip of the pyramid is gone!
Why that? Well, the pyramids are not standing on a flat plane, they are built on the top of a 40 meters high rocky cliff at the edge of the Nile Valley. And after one o'clock the shadow falls exactly into the valley, where even in the 19th Century a branch of the Nile flowed along (there are beautiful old romantic photos of sailboats right at the foot of the Great Pyramid - where the dial of the pyramid clock must have been)
.
At pharahonic times the situation was not different, because we know that a large harbor was immediately below the pyramid plateau.
In the morning the shadow runs for about 1 ½ kilometers through the desert until it is blocked by a natural hill where the shadow of the tip vanishes from sight. Only around 9:30 hours it reaches the plateau surrounding Giza and is usable for a dial. So this gigantic sundial would be usable at maximum for 3 ½ hours a day on four months. Sorry, this idea is pure nonsense.
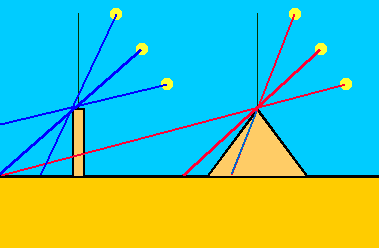
Why is a pyramid only usable for so few months in a year? Well, this is due to a property of the pyramid form. A stick always casts a shadow on the ground, as long as the sun is not directly above. This happens in southern Egypt for a few days of the year at noon.
In the drawing above it you can see, that the shadow cast by the third sun beam lies directly on the pyramid itself, it does not reach the ground.
At hhe Great Pyramid noo shadow is visible when the sun reaches an elevation of more than 52°. Around noon thisTo the Great Pyramid is therefore from a solar elevation of 52 ° no shadow visible. Around noon, this elevation is exceeded on 2/3 of the year ...
Formulations (b) und (c) make no sense at all. What is the “shadow length of a day”= And what surrounding tiles are meant? The plaster of the court is mostly gone so that we have no clue how it looked. Or does he mean the surrounding tombs of the nobles, the mastabas meant?
Dänikens völlig unsinnige Beschreibung des Rätsels zeigt, dass er (wie andere Kollegen auch) überhaupt nicht an dem interessiert ist, was er da abschreibt. Der Erfinder des Rätsels, Cotsworth, stellte die Behauptung auf, dass auf der Nordseite der Pyramide ein gepflasterter Hof angelegt worden sei, der bis in eine Entfernung von 90 Metern gereicht habe. Denn dies ist die maximale Schattenlänge der Pyramide zur Mittagszeit, die bei der Wintersonnenwende erreicht wird. Der Hof sei mit regelmäßigen Steinplatten belegt gewesen, und die Schattenlänge am Mittag, zum Südstand der Sonne, sei auf diesen Platten abgelesen worden. Sie hätten Auskunft über das genaue Tagesdatum, die herannahenden Sonnenwenden, Tag- und Nachtgleichen und die Nilflut gegeben. Dies bringt nun endlich Sinn in die verworrene Däniken-Beschreibung, und es klingt auch halbwegs logisch. Nur scheitert die Idee an drei unwesentlichen Kleinigkeiten:
The sundial theory has survived itself. Nevertheless, I consider briefly the other details given by von Däniken:
Formulation (b) and (c) are in the form of nonsense - what is please the "shadow length of a day"? And what surrounding slabs are meant? The foundation is irregular and available only in fragments. Or with "stone" surrounding the royal graves, the mastabas meant?
Däniken's completely nonsensical description of the puzzle shows that he (as well as other colleagues) not where is interested in what he copies since. The inventor of the puzzle, Cotsworth presented, based on the allegation that on the north side of the pyramid a paved courtyard has been created that have served up to a distance of 90 meters. For this is the maximum length of the shadow of the pyramid at lunchtime, which is reached at the winter solstice. The yard was covered with regular stone slabs, and the length of the shadow at noon, for Südstand the sun, had been read on these boards. They gave information about the precise date, the approaching solstice, day and night matches and the Nile flood. This has now finally in the confused sense Däniken description, and it sounds fairly logical. Only fails the idea of three insignificant trifles:
Inzwischen steht es beängstigenderweise 0:18 gegen die Dänikenschen Pyramidenmysterien.
Endergebnis: 0:19 gegen die Zahlenmysterien!!
Das ist das Fazit aus den vorgeführten 19 Zahlengeheimnissen. Ich habe noch weitere untersucht, mit ähnlichem „Erfolg“ wie hier. Die Hauptursache für das Versagen der Thesen ist darin zu sehen, dass viele von ihnen auf veralteten Zahlen und Messungen beruhen, und sich in den letzten 140 Jahren niemand auch nur die Mühe gemacht hat, diese zu überprüfen oder neue, auf modernen Werten beruhende Rätsel zu finden. Es ist schon seltsam. Da wird der Wissenschaft Dogmatismus und das Festhalten an „antiquierten Lehrmeinungen“ vorgeworfen - und ausgerechnet die Anhänger der progressiven Ideen verbreiten seit Anno Dunnemals veraltete Behauptungen als heute noch gültige Wahrheit! Wer hängt denn da an überkommenen Lehrmeinungen fest? That is the conclusion from the presented 19 Number secrets. I have also been examined. With a similar "success" as here The main reason for the failure of the theories is the fact that many of them based on outdated figures and measurements, and has in the last 140 years, no one even bothered to check these or new, based on modern values ??riddle find. It's strange. As the science dogmatism and detention is accused of "antiquated doctrine" - and just the supporters of progressive ideas spread since Anno Dunne times outdated assertions as still valid truth! He who loves for there fast to traditional doctrines?
Es gibt allerdings auch moderne Rätsel. Speziell seit der Entdeckung des „Marsgesichts“ in der Cydonia-Region auf dem Mars, sprossen neue Zahlenrätsel aus dem Boden, die die Pyramiden mit dem Sonnensystem in Verbindung bringen wollen. Mit kompliziertesten Berechnungen werden Karten des Sonnensystems in die Pyramiden projiziert, und sogar Karten des Gizeh-Plateaus über Bilder aus Sci-Fi-Filmen gelegt um kosmische Zusammenhänge zwischen Gizeh, Arthur C. Clarke und Stanley Kubrick zu finden. Eine der jüngeren „Entdeckungen“ beweist leider, dass auch diese modernen Pyramidenmystiker eines immer noch nicht beherrschen: Das Nachprüfen ihrer Quellen. So beglückte Holger Isenberg die Netzgemeinde mit folgender Erkenntnis (Tabelle von mir formatiert): There are also modern mystery. Especially since the discovery of the "Face on Mars' in the Cydonia region on Mars, new number puzzle sprouted from the ground, who want to bring the pyramid with the solar system together. With most complicated calculations maps of the solar system are projected into the pyramids, and even maps of the Giza plateau laid over images of sci-fi movies about cosmic connections between Giza, Arthur C. Clarke and Stanley Kubrick to find. A recent "discoveries" proves, unfortunately, that these modern mystic pyramid one rule still does not: The verifying their sources. Sun delighted Holger Isenberg the Internet community with the following conclusion (table formatted by me):
"Unglaublich!
Die Massenverhältnisse der Pyramiden stimmen nahezu exakt mit denen der 3 potentiell bewohnbaren Planeten im Sonnensystem überein!
Hat jemand eventuell exaktere Masse der Pyramiden? Ich fand auf die schnelle nur diese mit unbekannter Quelle:
Pyramide Volumen Größe % Khufu 481x775.75^2/3=96486686 f3 100% Khafra 471x707.75^2/3=78642880 f3 82% Menkaure 218x356.5^2/3=9235370 f3 10%
Planet Masse Masse % Erde 5.9736 x 1024 kg 100% Venus 4.869 x 1024 kg 82% Mars 6.4219 x 1023 kg 11%
Quelle:
Brian Crowley, Anthony Pollock: "Return To Mars"
Ursprünglich aber von Willy Kross.
Soweit Holger Isenberg. Während die Planetenmaße noch halbwegs stimmen, liegen die zur Erzeugung des Rätsels verwendeten Pyramidenmaße ganz schön daneben. Das Verhältnis der Planetenmassen beträgt[2]:
| MErde | 100 % |
| MVenus | 81,4 % |
| MMars | 10,7 % |
Die Pyramidenmaße[3]:
| Pyramide | Breite | Höhe | Volumen | % |
|---|---|---|---|---|
| Cheops | 230,36 m | 146,5 m | 2,591 Mio m3 | 100 % |
| Chephren | 215,25 m | 143,5 m | 2,216 Mio m3 | 85 % |
| Mykerinos | 104,60 m | 66,54 m | 0,242 Mio m3 | 9 % |
Prozentual sehen die Fehler minimal aus, rechnet man aber die Abweichungen von 3.6% bzw. 1.7% in Kubikmetern aus, erhält man Bauabweichungen von schlappen 93000 m3 bei der Chefrenpyramide und 44100 m3 bei der Mykerinos - Pyramide. Das entspricht Würfeln von 45 bzw. 35 m Kantenlänge. Im Vergleich zum Volumen der jeweiligen Pyramide muten die Fehler noch grotesker an, die 44100 m3 Baufehler der Mykerinospyramide entsprechen immerhin rund 20% des Volumens dieser Pyramide!!! Von bewusster Ähnlichkeit kann bei solch gigantischen Abweichungen keine Rede mehr sein. Sollten dies also wirklich Aliens „verbrochen“ haben, müssen diese ganz schön dumm gewesen sein :-) Percentage see the error of minimal, but reckoned from the deviations of 3.6% and 1.7% in cubic meters, obtained from slack Bauabweichungen 93,000 m 3 in the Chefrenpyramide and 44100 m 3 in the Menkaure - pyramid. This corresponds to 45 and 35 m cubes of edge length. Compared to the volume of each pyramid mute the errors even more grotesque, the 44,100 m 3 of construction errors Mykerinospyramide meet at least 20% of the volume of this pyramid! Conscious of similarity in such a gigantic deviations can be no question. So this should really have aliens "done wrong", they must have been pretty stupid :-)
Die Erklärung/Entschuldigung ließ nicht lange auf sich warten: Seien auch die Pyramidenmäntel berücksichtigt worden? Ja, sind sie :-) Und außerdem solle man genauere Daten verwenden, bei denen auch Hohlräume und die spezifischen Baumaterialien berücksichtigt seien. Nun, Hohlräume hat nur die Cheopspyramide, rund 1200 Kubikmeter oder 0.4% des Pyramidenvolumens. Da gibt's nix zu korrigieren. Und alle drei Bauten bestehen aus demselben Material, das sogar aus denselben Steinbrüchen stammt. Wie man es dreht und wendet: Ein neuer Schuss in den Ofen. The explanation / apology was not long in coming: Be taken into account the pyramid coats? Yes, they are :-) And also, one should use more accurate data, which also voids and specific materials are considered. Well, cavities has only the Great Pyramid, about 1200 cubic meters or 0.4% of the pyramid volume. There's nothing to correct. All three buildings are of the same material that comes even from the same quarries. As you look at it: A new shot in the oven.
Hans Jelitto, seines Zeichens Physiker und Mathematiker, Scientologe und beteiligt an der Planung des Mystery-Parks von Däniken, brachte vor einigen Jahren das Buch „Pyramiden und Planeten“ heraus, in dem auch er gar lustige Zusammenhänge zwischen den Pyramiden und Körpern unseres Sonnensystems herstellen wollte. Zu Zeiten des alten A.A.S.-Forums beschäftigte ich mich ein wenig damit, stellte aber schnell fest, dass er nicht anders vorging als seine numerologischen Brüder. Daher wollte ich mich eigentlich nicht weiter mit ihm beschäftigen.
Im Februar 2007 kontaktierte mich ein Leser seines Buchs und sprach mich auf eine These daraus an, die auf den ersten Blick wegen ihrer Genauigkeit überzeugend wirkt. Denn es soll die mittlere Pyramidengrundkante geteilt durch eine Lichtsekunde genau dem Erdvolumen geteilt durch das Sonnenvolumen entsprechen! Na, das wär ja was.
Hans Jelitto, his physicist and mathematician, Scientologist, and participated in the planning of the Mystery Park von Däniken brought a few years ago the book "pyramids and planets" out produce in the well, he does funny links between the pyramids and bodies of our solar system wanted. In the days of the old AAS forum I worked a bit with it, but noted quickly that he was not going on other than his numerological brothers. Therefore, I wanted to actually deal with it no more.
In February 2007, a reader contacted me his book and spoke to me on a thesis on it, which is convincing at first glance, because of their accuracy. For it is the middle pyramid base edge divided by a light second correspond exactly to the volume of soil divided by the volume of sun! Well, that would be so what.
Jelitto verwendete allerdings offenbar eine falsche Kantenlänge von 230,263 cm, anstatt der korrekten 230,36 cm[4]. Aber lassen wir das erst mal.
Der aktuelle Wert für Erdvolumen/Sonnevolumen ist 0,00000076711, die Kantenlänge der Pyramide durch die Vakuumlichtgeschwindigkeit mit Jelittos Wert 0,00000076805, mit dem Korrekten Wert 0,00000076818. In der Tat, die Fehler sind sooo minimal, dass man von einer Übereinstimmung ausgehen muss.
Jelitto used but apparently the wrong side length of 230.263 cm, instead of the correct 230.36 cm [ 4 ] . But let's leave the only times
.
The current value for soil volume / volume sun is 0.00000076711. The edge length of the Pyramid by the vacuum speed of light with Jelittos value 0.00000076805, with the correct value 0.00000076818 In fact, the errors are sooo minimal that you must take as a match.
Wirklich? Nein, denn Jelitto benutzt einen ganz einfachen Trick. Ein winziger Wert, geteilt durch einen riesigen Wert, gibt eine sehr kleine Zahl mit minimalst wirkenden Abweichungen. Eigentlich eine völlig sinnlose Darstellung. Interessant ist der Kehrwert: Wie oft passt die Erde in die Sonne, und die Pyramidengrundseite in die Lichtsekunde!
Schauen wir uns mal das Ergebnis an: In ein Sonnenvolumen passen 1.303.600 Erdvolumen hinein, in eine Lichtsekunde allerdings 1.301.999 bzw. 1.301.773 Pyramidenkantenlängen. Die Differenz beträgt 1601 (Jelittos Basisbreite) bis 1827 Erdvolumen! Das ist kein Rundungsfehler mehr.
Man kann übrigens auch berechnen, wie breit die Pyramide denn sein müsste, um das Rätsel zu erfüllen. Man staune: 228,22 Meter, das liegt nahe an den Schätzungen, die Smyth damals für seine allerersten Spielchen verwendete.
Aber - nein, Jelitto wird doch nicht??? Oder doch...
Really? No, because Jelitto used a very simple trick. A tiny value, divided by a huge value there, a very small number of minimally acting discrepancies. Actually a completely meaningless representation. Interesting is the inverse: how often the earth fit in the sun, and the pyramid base side in the light second
!
Let's look at the result: In a sun-volume fit into 1,303,600 soil volume, but in a light-second or 1,301,999 1,301,773 pyramid edge lengths. The difference is 1601 (Jelittos base width) and 1827 volume of the earth! This is no rounding errors.
You can also submit calculate how wide the pyramid would have to be because, in order to meet the mystery. It's amazing: 228.22 meters, which is close to the estimates that were used at that time for his first ever Smyth
games.
But - no, Jelitto is not? Or is it ...