

Im Jahr 2002 ist zu den schon besprochenen Pythagoras-Thesen eine neue dazugekommen. Erneut behauptete ein Autor, das Rätsel der Gizeh-Pyramiden gelöst zu haben. und ein mathematisches Modell entdeckt zu haben. Der Autor Klaus Schröer war sich seiner Sache auf seiner inzwischen gelöschten Web-Präsemz absolut sicher. Zu Recht?
Der Autor und seine These sind inzwischen in Vergessenheit geraten, da seine Argumentation und später seine lustigen Entschuldigungen allerdings so szenetypisch sind, finde ich es sinnvoll, sie hier vorzustellen.
Auf einer Landkarte des Gizeh-Plateaus, angefertigt von Napoleons Wissenschaftlern während des unglücklichen Afrikafeldzugs von 1798 bis 1801, entdeckte Schröer einen seltsamen Zusammenhang:
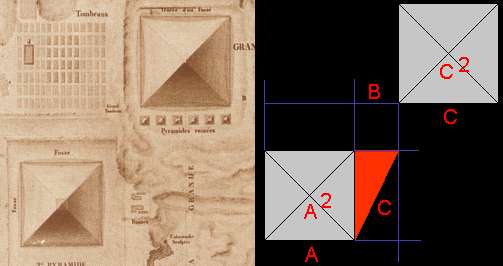
Der Abstand zwischen der Ostseite der Chefrenpyramide der Westseite der Cheopspyramide ist exakt so groß, dass die längste Strecke (Hypotenuse) des eingezeichneten roten rechtwinkligen Dreiecks genauso groß ist wie die Basislänge der Cheopspyramide. Was kann das bedeuten?
|
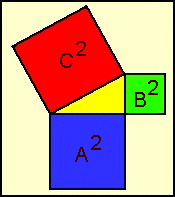
| Fig. 2 - Satz des Pythagoras |
In einem rechtwinkligen Dreieck ist die Fläche der beiden Quadrate, die man mit den an den rechten Winkel grenzenden Seiten bildet (A und B) zusammengenommen genauso groß wie das Quadrat der längsten Seite C. In der Anordnung, die Schröer gefunden zu haben scheint, ist wie oben beschrieben der Abstand zwischen den beiden größten Pyramiden in Ost/West-Richtung genauso groß um daraus ein entsprechendes Dreieck zu bilden. Die Seite A ist dabei direkt die Basis der Chefrenpyramide. Die Seite B ist die Abstandslinie Cheops/Chefren, und die Basisbreite der Cheopspyramide selbst findet sich wieder in der längsten Seite (Hypotenuse) des roten Dreiecks.
Praktisch zur Bestätigung haben die Ägypter dann noch die kleinste, die Mykerinospyramide gebaut, deren Fläche auch exakt B2 entspricht.
Um dies zu belegen führt Schröer eine detailliert geschilderte geometrische Konstruktion durch, in der er allerlei Zirkelschläge und Hilfsdreiecke konstruiert. Der Weg ist so komplex, dass ein Laie kaum noch durchsteigt. Aber warum so kompliziert?
Die Überprüfung geht viel, viel einfacher und viel, viel schneller. Sollte der Zusammenhang stimmen, erhält man den notwendigen Abstand B der Pyramiden durch eine ganz einfache Berechnung. Wenn A2 + B2 = C2 ist, erhält man B indem man die Quadratwurzel aus C2 - A2 zieht. A2 ist nichts anderes als die Basisfläche der Chefrenpyramide, C2 steht für die Fläche der Cheopspyramide. Zieht man also beide Grundflächen voneinander ab erhält man mit B2 die Fläche eines mit der Strecke B konstruierten Quadrates. Zieht man daraus die Wurzel, erhält man die Länge der Strecke die notwendig wäre, um diese Bedingung zu erfüllen. Das Resultat dieser Berechnung kann man anhand der Realität überprüfen.
Die Basisbreite der Cheopspyramide beträgt 230 Meter (auf Zentimeterwerte verzichte ich der Einfachheit halber), und die der Chefren-Pyramiden 215 Meter. Die Differenz der Flächen beträgt 6675 Quadratmeter, die Quadratwurzel davon ist 81.7 Meter. Dies ist die notwendige Länge der Strecke B.
Zur Überprüfung dieser Strecke habe ich einen 1:2000-Plan des Giseh-Plateaus herangezogen[ 1 ]. Mit einem Maßstabslineal lässt sich hier problemlos eine Genauigkeit von einem Meter erreichen. Die Entfernung gemäß dieser Karte beträgt - knappe 110 Meter!!!. Ende, aus, Schluss. Knappe 30 Meter Fehler auf einer Stecke von rund 100 Metern, da kann man sich nicht mit Baufehler herausreden. Mehr muss man zu dem Thema eigentlich nicht sagen. Die Sache hat sich erledigt.
Den Fehler kann an übrigens auch ohne Wurzelberechnungen finden (falls man keinen Taschenrechner zur Hand hat): Gemäß der geometrischen Konstruktion des Verfassers muss der Nord/Süd-Abstand der Cheops- und Chefrenpyramide exakt gleich der Basisbreite der Cheopspyramide minus dem Ost/West-Abstand beider Pyramiden sein. Also 120 Meter. Der wahre Abstand beträgt aber mehr als 130 Meter.
Die Schnellüberprüfung hat ergeben, dass die These nicht stimmen kann. Warum hat der Autor solch eine Überprüfung nicht selbst durchgeführt? Nun, er hatte, wie seiner Homepage zu entnehmen war, zwar genug Interesse am Thema um (einmal wieder) das Weltbild der Ägyptologie umkrempeln zu wollen, aber anscheinend wenig bis kein Interesse daran, wertvolle Zeit mit recherchieren zu verschwenden. So waren die Napoleonkarte und ein leicht verzerrtes Satellitenphoto offenkundig die einzigen Quellen die ihm zur Verfügung standen. Und auf diesen stimmt alles. Behauptet er.
|
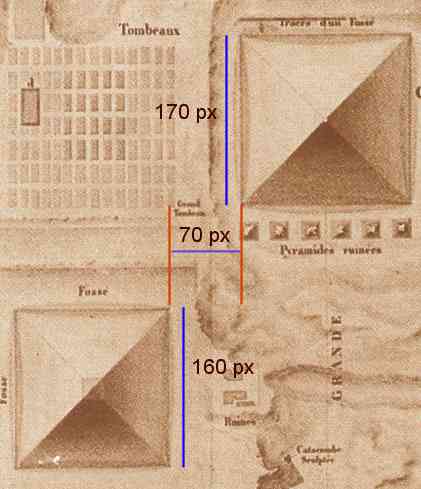
| Fig. 3 - Strecken auf der Napoleon-Karte |
Wirklich? Nun, selbst wenn auf den Karte kein Maßstab verzeichnet ist, kann man auch auf ihnen eine Abschätzung durchführen. Ich habe auf der bei Schröer ursprünglich gelinkten Napoleon-Karte einfach die Basislängen der Pyramiden und den Abstand in Pixeln (px) gemessen. Cheops 170 Pixel, Chephren 160 Pixel, Distanz 70 Pixel. Distanz2 wäre 4900, (Cheops2 - Chephren2) ergibt aber den Wert von 3300. Die Quadratwurzel daraus ist 57.4, knapp 13 Pixel oder 20% zu kurz! Schon auf der vom Autor verwendeten Karte (die nicht gerade die Ausgeburt an Präzision ist) lässt sich die These also in wenigen Sekunden rechnerisch widerlegen.
Auch beim Satellitenbild von Spaceimaging klappt es nicht besser. Ich habe aus Neugier das Bild in voller Auflösung (Achtung! 3 MB groß!) heruntergeladen und die Messwerte wie bei der Napoleonkarte ermittelt. Herausgekommen sind dabei: Cheops 277 -283 Pixel (die Pyramiden sind perspektivisch gestaucht), Chefren 265 Pixel, Abstand der Pyramiden 150 Pixel. Setzt man die Pyramidenseiten in die oben genannte Gleichung ein, erhält man aber einen notwendigen Abstand von 80-99 Pixeln! Auch auf dieser Karte funktioniert die Gleichung offenkundig nicht.
Eigentlich hätte ich an der Stelle erwartet, dass der Autor zugibt "OK, stimmt halt nicht, hab mich vertan". Aber so funktioniert die Grenzwissenschaft nicht, denn die hat immmer Recht. Und wenn nicht, hat irgendwie die pöse Wissenschaft Schuld. So auch hier, der Autor weigerte sich hartnäckig, irgend einen Fehler einzusehen und brachte ein Bündel abstruser Erklärungsversuche, von denen ich einige exemplarisch vorstelle:
|
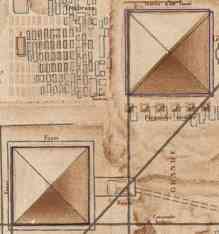
| Fig. 4 - Lehner und Napoleon |
Die Pyramidenmaße in der modernen Literatur seien falsch, argwöhnte der Autor. Lediglich die Napoleonkarte sei korrekt, alle späteren Forscher seien bereits ideologisch vorgefärbt an die Messung herangegangen und hätten die Werte verfälscht, da sie lediglich vorgefasste Thesen belegen wollten, und natürlich das überlegene Wissen der alten Ägypter vertuschen wollten. Wäre die große Pyramide in Wirklichkeit ein paar Meter größer, wie es auf der Napoleonkarte sei, wäre alles bestens.
Nun, in dem nebenstehenden Bild habe ich einmal die Napoleonkarte und eine moderne Karte (Lehner, The Complete Pyramids) zur Deckung gebracht. Seltsam: Die Pyramidenmaße beider Karten stimmen recht gut überein (die modernen Maße sind 2,5 m kleiner als die von Napoleon ermittelten, die Abweichung ist kleiner als die Liniendicke auf der Karte), lediglich die Position der Pyramiden sind leicht verschoben (die moderne Karte setzt die Pyramide um ca. 12 Meter nach Osten und ungefähr 8 Meter weiter nach Süden).
Die Abweichugen sind viel zu gering, als dass Schroer daraus irgendwelche Vorteile ziehen könnte.
Irgendwann hatte Schroer gemerkt, dass er so nicht weiter kam. So meinte er dann, das wir heute doch überhaupt nicht wissen, wie groß die Cheopspyramide wirklich war. Steinräuber hätten die Dimensionen verändert. Wenn die Cheopspyramide zum Beispiel nur 11 Meter breiter gewesen wäre als heute, würde alles prima passen. Noch besser: Wenn sie nur in West- und Nordrichtung größer gewesen wäre, reichten durch die gleichzeitige Verringerung der Distanz 8 Meter. Wenn heute eh' schon 6 Meter fehlen (durch den Steinklau ist die Pyramide im Schnitt nur noch 224 m breit) , könnten es wohl durchaus auch 14 Meter gewesen sein.
Der Autor nennt auch ein Argument für den von ihm vermuteten einseitigen Steinabtrag: Die Nord- und Westseite der Pyramide sei am kühlsten und schattenreichsten, Steindiebe hätten sich daher bevorzugt dort aufgehalten.
Wenn man auf der Basis anfängt, mit "vielleicht"'s und "möglicherweise"'s zu argumentieren kann man letztlich jede Wunschthese erklären. Wissenschaftlich gesehen ist eine solche Argumentation wertlos.
Natürlich gibt es aber auch Gründe dafür, warum die Archäologen auf die entsprechenden Werte kommen. Denn es liegen rings um die Pyramidenbasis noch etliche Verkleidungssteine in Situ - und das bei praktisch allen Pyramiden. Zur Zeit des großen Steinraubs waren die Pyramiden metertief zugeweht, und die Steindiebe haben sich oft nicht die Mühe gemacht, sich bis zum Fundament durchzugraben. Lediglich die überirdischen Bereiche wurden geplündert. Nachfolgend einige Bilder.


Links eine Übersicht über die Westseite der Cheopspyramide, rechts einige erhaltene Verkleidungsblöcke dort. Zu den erhaltenen Verkleidungsblöcken kommen noch Anrisslinien der Pyramidenbauer, die zur Einmessung dienten und auf langen Strecken noch erhalten geblieben sind:



Ganz links ist ein Bild mit Verkleidungsblöcken und Messlinien von der Westseite der Cheopspyramide abgebildet. In der Mitte ist der größte erhaltene Verkleidungsblock an der Nordseite der Pyramide abgebildet - 15 Tonnen schwer und noch dort wo ihn die Erbauer hingesetzt haben. Ganz rechts ist ein von den Arabern malträtierter Granitverkleidungsblock der Chephren-Pyramide zu sehen. Abschließen möchte ich diesen kleinen Exkurs mit der am besten erhaltenen Reihe von Verkleidungsblöcken an der Nordseite der Cheopspyramide:

Während der Borchardt-Grabungen 1925 wurden erstmals alle Seiten der Cheopspyramide partiell freigelegt und die dort erhaltenen Linien zur genauen Vermessung verwendet. Der mit den Vermessungen beauftragte Ingenieur J.H. Cole fasst den Befund der Seiten zusammen:[2 ]
Dorner führte 1980 eigene Messungen durch, speziell auf der unter Bochardt noch unzureichend freigelegten Westseite (die für diese These hier ausgerechnet von besonderem Interesse ist). Dorner vermerkt dazu:
"Auf der Westseite finden sich sowohl in der Nähe der Nord- als auch der Südecke größere Pflasterreste... Etwa in der Mitte der Seite ist auf eine Länge von etwa 60m die Anritzung am Pflaster deutlich sichtbar, außerdem befinden sich dort noch zahlreiche Blöcke der Verkleidung in ihrer ursprünglichen Lage. ..."[3 ]
Dorner konnte das Ergebnis des Kantenwinkels Coles um 20" verbessern und fand ansonsten seine Ergebnisse bestätigt. Der Restfehler an der großen Pyramide dürfte heutzutage auf keiner Seite einen Zentimeter überschreiten.
Es gibt, glaube ich, keinerlei Zweifel daran, dass eine Verbreiterung der Pyramide, egal in welcher Richtung, gänzlich ausgeschlossen ist.
Die letzte Ausrede die ich hier vorstellen will, übertrifft an Skurrilität wirklich alles bisher Gehörte. Der Autor meinte nämlich, dass der Abstand zwischen den Pyramiden durch tektonische Aktivitäten ja heute ein anderer sein könnte als noch vor 4500 Jahren.
Nun, wir sprechen hier nicht um Ungenauigkeiten von ein paar Zentimetern, sondern von rund 30 Metern!!! Und wie stellt sich der Autor das vor? Meint er, dass Felsen wächst wenn man ihn kräftig gießt? Derartige Phänomene treten nur an Schollengrenzen auf, zum Beispiel auf Island. Oder an Verwerfungszonen wie der berühmten San-Andreas-Spalte in Kalifornien. Aber dort entstehen bei derartigen Bewegungen deutliche Spuren. Verschieben sich die Schollen gegeneinander, entstehen Verwerfungslinien, sonst gibt es Auffaltungen, Grabenbrüche oder Vulkanismus. Zu beobachten im Oberrheingraben, auf Island, in den Alpen, im Rift Valley und auf dem mittelatlantischen Rücken. So etwas wäre unübersehbar
Auch diese Ausrede kann nicht überzeugen.
Wieder einmal wurde mit großem Tamtam die "Lösung" aller offenen Fragen zum Giseh-Plateau angekündigt, und wieder einmal erwies sie sich als Luftschloss. Die Beschäftigung mit den Ausreden des Verfassers nimmt ja sogar mehr Platz ein als die eigentliche Widerlegung der These selbst. Die Fehler sind mit bloßem Auge sichtbar (z.B. die fehlerhaften Streckenverhältnisse) oder durch eine simple mathematische Operation aufzuspüren. Die Ausreden über ideologische Messungen oder fehlerhafte Pyramidenbreiten sind bereits mit Grundkenntnissen zu den Pyramiden zu widerlegen, die wandernden Pyramiden benötigen lediglich ein wenig "gesunden Menschenverstand".
Natürlich war de Autor empört über meine Besprechung. Wieder ein Betonkopf, der das große Bild und die spirituellen Zusammenhänge mit dem Universum nicht erkennt.
Genau, 42.
| Anmerkungen: | ||
| [1 ] | Maragioglio & RinaldiL'Architettura..., Vol. VI Tavola Tafel 1 | |
| [2 ] | Dorner, Josef; Die Absteckung und astronomische Orientierung ägyptischer Pyramiden, S. 70, 71, Übersetzung der Passagen FD. | |
| [3 ] | ibd. S. 75 | |